みなさん、こんにちは。Google Cloud Solutions Architectの中井です。
HTML5 Conference 2016では、「Webアプリケーションにおける機械学習活用の基礎」と題して、機械学習の基礎となる仕組み、そして、機械学習を利用したクライアントアプリケーションの例を紹介させていただきました。今回は、この発表の内容を振り返りたいと思います。

機械学習とディープラーニング、そして、AIの関係
機械学習そのものは古くから利用されている技術であり、過去のデータを元にして、「(まだ見たことのない)未来のデータにもあてはまる一般的なルール」を発見することがその役割となります。つまり、はじめて見るデータに対して、何らかの予測を立てることができるようになります。たとえば、映画のレコメンデーションシステムであれば、新しいユーザーのプロファイルデータから、そのユーザーが高い評価を付けるであろう作品を予測します。
ただし、これはあくまでも予測ですので、必ず正解するというわけではありません。予測の精度をいかに上げるかが機械学習の課題となります。そして、近年のディープラーニングの発展により、一部の領域においては、その予測精度が格段に向上しました。プロの棋士と同等、あるいは、それを上回る精度で「勝利につながる一手」を予測する囲碁プログラム、本物の人間であるかのように、あるメッセージに対する「自然な応答メッセージ」を予測するチャットボットなど、中の仕組みを知らない人間からすると、あたかもコンピューターが「知性」を持っているかのように感じられるレベルにまで達しています。
ちなみに、最近、各種メディアでは、「AI(人工知能)で◯◯を実現」というタイトルを目にすることがあります。しかしながら、何を指して「AI(人工知能)」と呼んでいるのかが曖昧なことも少なくありません。AI(人工知能)もまた長い歴史を持つ研究分野であり、AI(人工知能)の定義にもいくつかのパターンがあるようですが、現代的な文脈では、「あたかも知性を持っているかのように感じられる製品やサービス」を指して、AI(人工知能)と呼んでいると考えるのが適切かもしれません。
そのような製品・サービスを実現する上で、高い精度での予測を実現するディープラーニングは、欠くことのできない中核技術になりつつあるということでしょう。(これは余談ですが、個人的には、「AI(人工知能)で◯◯を実現」というタイトルを見るたびに、心の中でそっと、「AI(知性を持ったかのように見える製品やサービス)を実現するために研究・活用が進んでいる機械学習を基礎とした一連のデータ収集・分析技術で〇〇を実現」と読みかえて納得することにしています)

「線形2項分類器」で機械学習の基礎を学ぶ
この発表では、まずはじめに、機械学習の基礎となる「線形2項分類器」、そして、それを実現する「ロジスティック回帰」のアルゴリズムを解説しました。下図のように平面ちらばった◯✕の2種類のデータに対して、これらを分類する直線を自動的に見つけ出すという問題です。
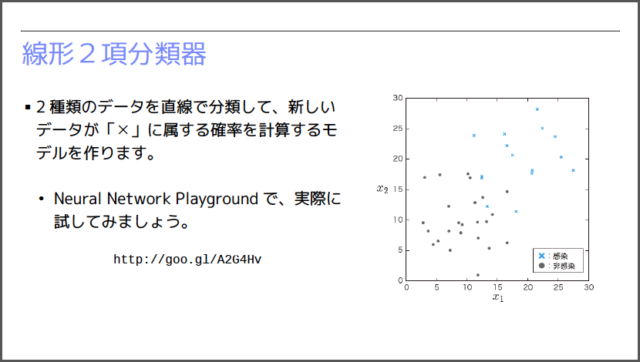
そして、機械学習の世界では、主に「確率」を用いた予測が行われます。下図のように、求めるべき直線を関数 f で表した後に、ロジスティック・シグモイド関数 σ を用いて、「あるデータが『✕』のタイプである確率」を計算します。この計算式には、未知のパラメーター(w0, w1, w2)が含まれており、既存のデータに対する予測精度が最大化されるように、これらのパラメーターを自動調整するということを行います。
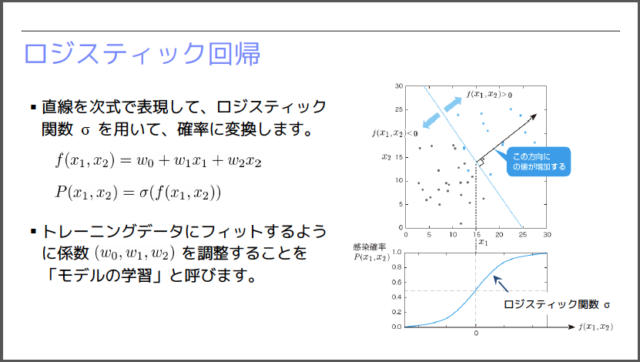
自動調整に用いられるアルゴリズムの詳細は、ここでは割愛しますが、たとえば、「Neural Network Playground」を利用すると、実際のチューニングの様子を観察することができます。これは、TensorFlowの動作をJavaScriptでエミュレーションしたもので、機械学習の処理が進む様子をブラウザー上で観察することができます。会場では、参加者の方々にも、実際にリンクを開いて機械学習の動作を体験していただきました。
「線形多項分類器」で文字認識に挑戦
先ほどの例では、◯✕の2種類のデータを分類しましたが、これをより多数の種類に分類できるように拡張したものが「線形多項分類器」です。たとえば、3種類に分類するのであれば、下図のように、3つの1次関数を用意します。そして、どの1次関数の値が最も大きいかによって、領域を分類します。ちなみに、(x1,x2)平面上で1次関数がとる値を3次元のグラフに表すと、1枚の平面になります。したがって、3枚の平面を配置して、どの平面が一番上に来るかで領域を分類していると考えることができます。
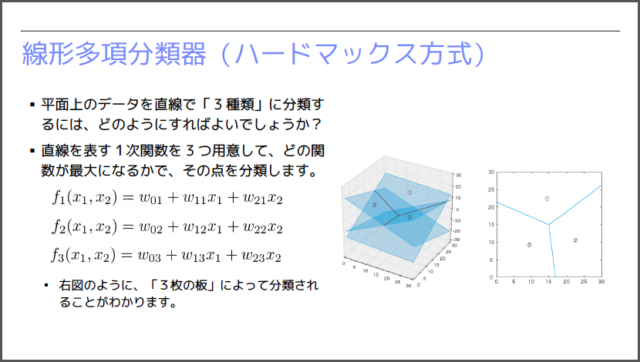
ただし、前述のように、機械学習の世界では「確率」で予測を行う必要があります。それぞれの1次関数の値を0〜1の確率に変換するのが、下図の「ソフトマックス関数」です。ここでは、簡単化した1変数の例を図示してありますが、f1, f2, f3の値の大小関係が、きれいに確率の大小関係に変換されていることがわかります。会場では、この仕組みを用いて、画像データの分類を行うデモを紹介しました。
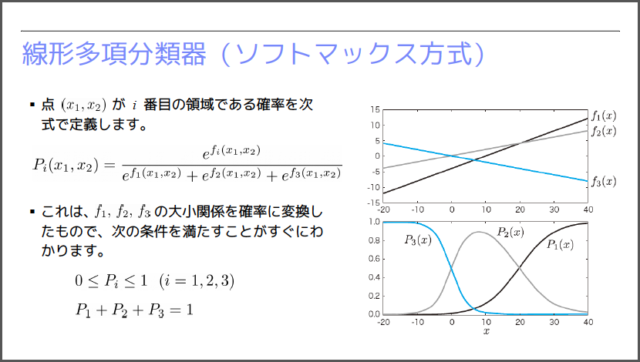
ここで使用したのは、MNISTデータセットと呼ばれる手書き数字の画像を集めたデータセットです。それぞれが28✕28=784ピクセルのグレイスケールの画像になっており、1つの画像データは、784個のピクセル値(各ピクセルの濃度の値)からなります。そして、784個のピクセル値からなるデータは、784次元空間の1つの点に対応すると考えることが可能です。
いきなり784次元空間が登場して驚くかも知れませんが、それほど難しい話ではありません。3次元空間の点は、(x,y,z)の3つの数値で指定することが可能です。これと同じように、784次元空間の点は、784個の座標値で指定することができます。そして、大量の画像データを784次元空間にばらまくと、下図のように、同じ数字の画像は互いに近くに集まって、クラスターを形成すると想像することができます。
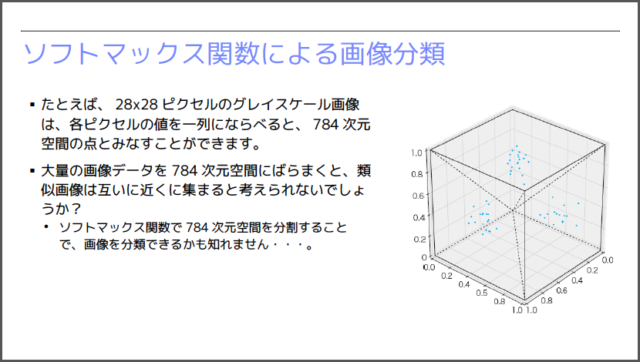
仮にこの想像が正しければ、線形多項分類器を用いて、784次元空間を10ヶ所の領域に分割することで、画像の分類が可能になります。新しい画像データが与えられた場合は、それがどの領域に入るかによって、どの数字であるかを予測することができます。
下図は、TensorFlowを用いて実装したコードで実際に分類を行った結果です。ここでは、トレーニング用のデータセットで学習した後に、テスト用のデータに対して予測を行っています。正解例だけを見ていると優秀な結果にも見えますが、不正解例を見ると、わりと単純なミスを犯していることもわかります。
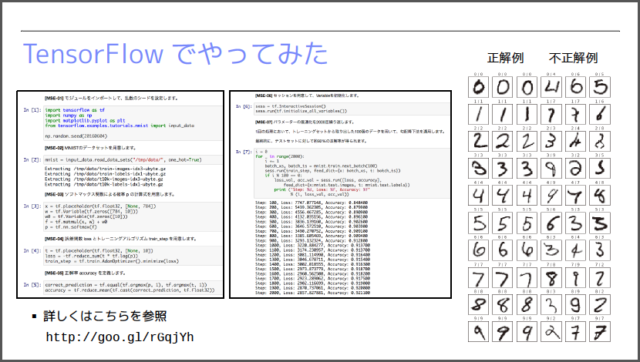
これは、ピクセルの配置情報だけを用いて分類を行っていることが原因です。たとえば、上図における、上から2段目の右端の例が特徴的です。この縦長の「6」は、ピクセルの並びだけを見ていると「1」に近いため、「1」であると誤分類されています。人間が数字の種類を判別する際は、単純なピクセルの並びだけではなく、「穴が空いている」などの空間的な情報も利用します。この分類の精度を向上するには、このような、ピクセルの並び以外の特徴を取り出す必要があるのです。
「畳込みニューラルネットワーク」による性能向上
画像認識において、画像の空間的な特徴を取り出すのに役立つのが「畳込みフィルター」です。下図に示す「畳込みニューラルネットワーク(CNN:Convolutional Neural Network)」では、事前に畳込みフィルターを用いて、画像の特徴を抽出した後に、それを用いて多項分類器(ソフトマックス関数)による分類処理を行います。
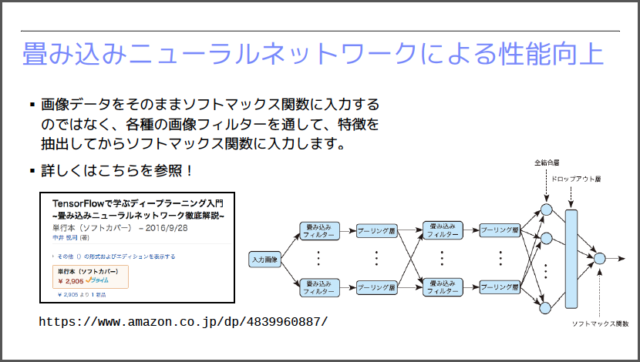
ただし、どのようなフィルターを用いれば、分類に役立つ特徴が抽出できるかを考えるのは簡単ではありません。実は、CNNでは、フィルターを構成するパラメータ値も機械学習の対象としてしまいます。はじめは、乱数で用意したフィルターを用いて判別処理を行います。当然ながら、判別精度はそれほど高くありません。この後、判別精度が向上するように、フィルターのパラメータ値を自動的に調整していきます。
会場では、この処理を実行するTensorFlowのコードを紹介した上で、学習結果を用いた簡易的な「手書き文字認識アプリ」をデモで紹介しました。下図は、入力画像に対して、「0」〜「9」のそれぞれの数字である確率を表示している例になります。
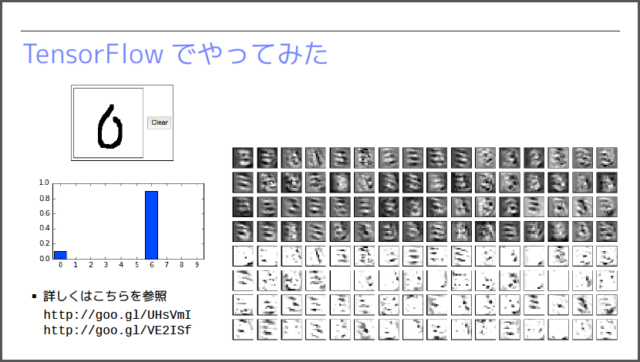
参考資料
当日の発表では、このような機械学習を活用したアプリケーションの例、あるいは、今後想定される利用パターンなども紹介させていただきました。興味のある方は、当日の発表資料を参考にしてください。
また、発表の中では、線形多項分類器やCNNのパラメータを自動調整するアルゴリズムの解説までは手が回りませんでした。これらの理論的背景に興味のある方は、下記の書籍も参考にしていただければ幸いです。
- ITエンジニアのための機械学習理論入門 中井悦司(著)(技術評論社)
- TensorFlowで学ぶディープラーニング入門 中井悦司(著)(マイナビ出版)
